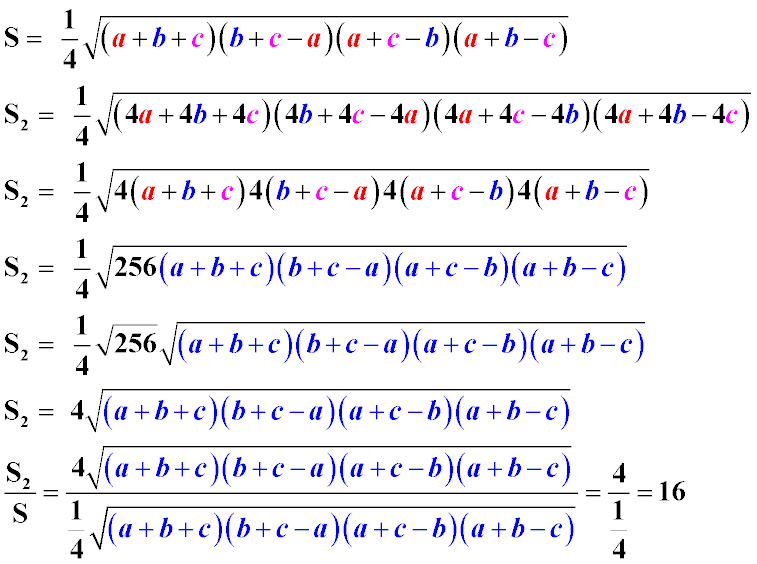Как найти площадь

Общая формула

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

S = 0,5 * a * h, где a — основание, h — высота.

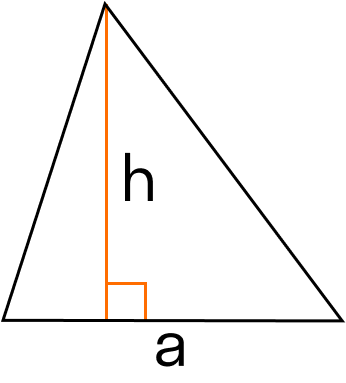
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

S = a2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

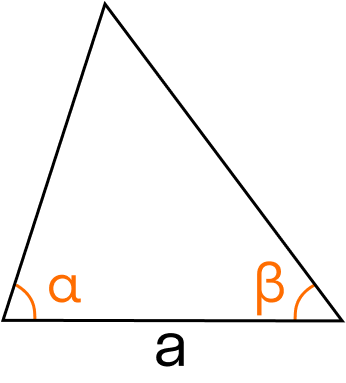
6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c)​, где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Примеры решения задач

Задача

Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁.

Рисунок 3

Дано: AB = 3, A₁B = 6, AD = 5.

Решение

Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA₁. Так как длина диагонали A₁B известна, сделать это нетрудно.

Воспользуемся теоремой Пифагора:

\(A_1B=\sqrt{{AA_1}^2+{AB}^2}\)

Соответственно, \({AA_1}=\sqrt{{A_1B}^2-{AB}^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{25}=5\)

Подставим известные значения в формулу расчета площади поверхности:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

\(S=2\cdot(AB\cdot AD+AB\cdot AA_1+AD\cdot AA_1)=2\cdot(3\cdot5+3\cdot5+5\cdot5)=2\cdot(15+15+25)=2\cdot55=110\)

Ответ: S=110.

Задача 2

Вычислить длину стороны прямого параллелепипеда ABCDA₁B₁C₁D₁.

Рисунок 4

Дано: S_пов=96, S_бок=60, b=6.

Решение

Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:

\(S=a\cdot b\)

Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:

\(S_{пов}-S_{бок}=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c-2\cdot a\cdot c-2\cdot b\cdot c=2\cdot a\cdot b\)

Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:

\(2\cdot a\cdot b=S_{пов}-S_{бок}\)

\(a=\frac{S_{пов}-S_{бок}}{2\cdot b}=\frac{96-60}{2\cdot6}=\frac{36}{12}=3\)

Определение понятия

Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.

Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.

Единицы измерения площади

В одном квадратном сантиметре сто квадратных миллиметров

Метрические единицы

• Квадратный метр, производная единица Международной системы единиц (СИ); 1 м² = 1 са (сантиар);
• Квадратный километр, 1 км² = 1 000 000 м²;
• Гектар, 1 га = 10 000 м²;
• Ар (сотка), 1 а = 100 м²:
• Квадратный дециметр, 100 дм² = 1 м²;
• Квадратный сантиметр, 10 000 см² = 1 м²;
• Квадратный миллиметр, 1 000 000 мм² = 1 м²;
• Барн, 1 б = 10−28 м².

Русские устаревшие

• Квадратная верста = 1,13806 км²
• Десятина = 10925,4 м²
• Копна = 0,1 десятины — сенные покосы мерили копнами
• Квадратная сажень = 4,55224 м²

Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, верёвка, жеребья и др.

Другие

• Рай = 1600 м² (40 м × 40 м).
• Квадратный парсек
• Планковская площадь (SP,ℓP2{\displaystyle S_{P},{\ell }_{P}^{2}}) ≈ 2,612099 · 10−70 м2

Как посчитать площадь стен комнаты?

Ознакомьтесь также с этими статьями

• Внутренняя отделка домов гипсокартоном

• Основные виды и особенности современных отопительных котлов для частного дома

• Верный помощник в борьбе с ненужной травой или порослью

• Квартиры в новостройке по доступной стоимости

Чаще всего стены в комнатах простой, прямоугольной формы. Для подсчета их площади существует две легких формулы:

S = P x h,

P = (a + b) x 2.

Где,

• S – площадь;
• P – периметр;
• h – высота поверхности;
• a – ширина помещения;
• b – длина помещения.

Интересно!
В техническом паспорте помещения обычно указывается площадь и периметр, как всего помещения, так и отдельных комнат. Так что можно эти данные уточнить там.

Сначала измеряется ширина и длина помещения по плинтусам. Высота измеряется обычно в углу. Например, если a = 6 м, b = 5 м, h = 3 м, то P = (6 + 5) х 2 = 22 м. После этого можно узнать и площадь:

S = 22 х 3 = 66 м².

Калькулятор площади пола

Чтобы не мучиться с ручными расчетами на бумаге и не осваивать компьютерные программы, можно воспользоваться помощью онлайн-калькуляторов. Такую возможность предоставляет масса Интернет-ресурсов. В специальном окошке достаточно ввести все данные, и после нажатия кнопки «рассчитать» в новом поле или на новой странице откроются итоговые посчитанные данные. Обычно все показатели вводятся в метрах, но по желанию можно указать и другие единицы измерения.

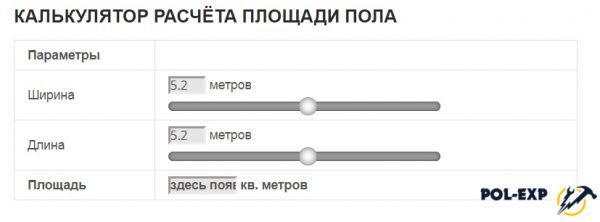
У онлайн-калькуляторов есть свои плюсы и минусы

Достоинства онлайн калькуляторов:

• не нужно считать вручную;
• можно легко получить площадь любой фигуры;
• скорость расчетов и их точность высоки.

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

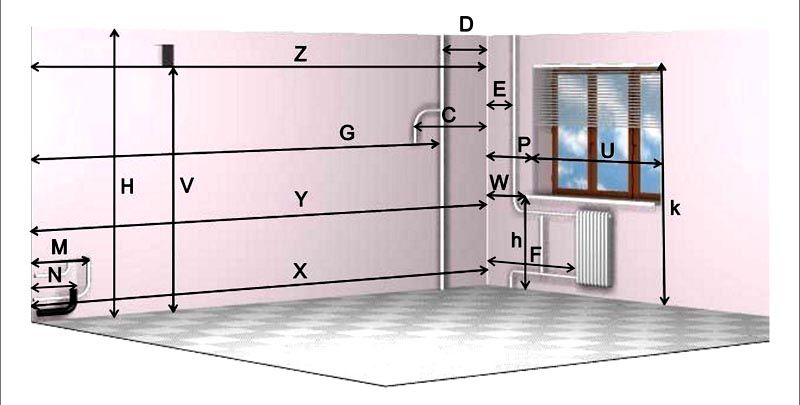Особенности замеров с учетом линий коммуникаций

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз. Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Лазерное приспособление заметно облегчает работу

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

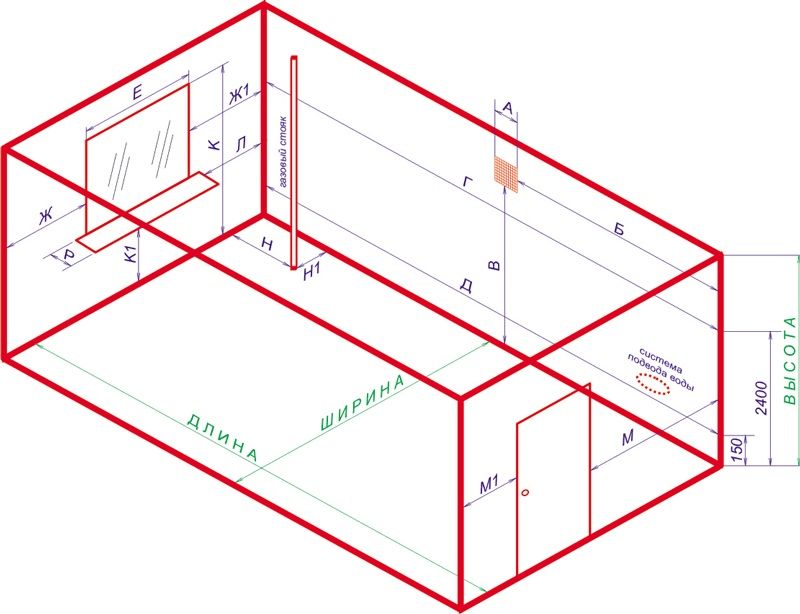На схеме показаны все необходимые замеры для правильных расчетов

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето  —  прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно  —  от дробей до синусов —  и ответят на вопросы, которые бывает неловко задать перед всем классом.

Точность расчетов площади

При определении площади участка необходимо учитывать погрешности расчета площади.

В частности, если площадь участка рассчитана по координатам поворотных точек, то разница между расчетным и зафиксированным в ЕГРН значениями площади ЗУ не должна быть больше допустимой величины (dSдоп).

В нормативных документах эта величина определена следующим образом:

• Mt — погрешность (СКП) расположения поворотной точки,
• Sy-площадь участка.

Если же dS оказывается меньше допустимого значения, то за окончательное значение площади может быть принято расчетное значение площади с указанием допустимого значения dPдоп.

Пример.

Вычисленная площадь участка № 103 снт «Изобретатель» составила 594 кв. м. По документам площадь участка равна 600 кв. м.

СКП Мt при межевании для садоводческих товариществ определена нормативно (приказ МЭР №518) и равна 20 см. Тогда:

dS = 600-594= 6 кв. м

dSдоп=3,5*0,2* √600=17,14 кв. м

Окончательное значение площади участка №103 Sy=594±17 кв. м.

Дорогие читатели, информация в статье могла устареть, воспользуйтесь бесплатной консультацией позвонив по телефонам: Москва +7 (499) 653-60-87 , Санкт-Петербург +7 (812) 313-26-64 или задайте вопрос юристу через форму обратной связи, расположенную ниже.

Расчет площади земельного участка Варианты аналитического способа расчета площадей для земельных участков различных геометрических форм. Формулы расчета по координатам поворотных точек.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 м². В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 м².
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 м².
3. Складываем две величины: 30,6 м². + 2,6 м². = 33,2 м².

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 м². Если округлить, получим 9, 0 м².
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 м². Округляем, получаем 5,1 м².
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 м². После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 м².

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

1. Найти квадрат диагонали (умножить диагональ на саму себя).
2. Найти половину этого квадрата – умножить его на 0,5.
3. Найти синус угла между диагоналями.
4. Умножить половину квадрата диагонали на синус угла между диагоналями.

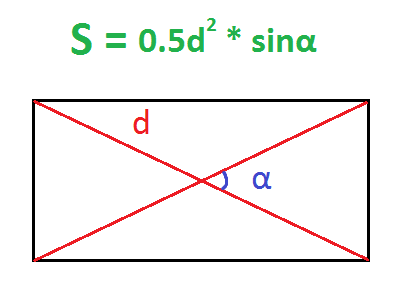
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

1. Квадрат диагонали: 10*10 = 100 см.
2. Половина этого квадрата: 0,5*100 = 50 см.
3. Синус угла между диагоналями: sin 30 градусов = 0,5.
4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Как рассчитать площадь комнаты — задача для первоклассников

Что может быть про­ще рас­че­та пло­ща­ди пря­мо­уголь­ни­ка? Ведь это самая пер­вая и про­стая зада­ча из учеб­ни­ка гео­мет­рии для пер­во­го класса.

• Изме­ре­ние про­во­дим при помо­щи стро­и­тель­ной рулет­ки с фик­са­то­ром, жела­тель­но у плин­ту­сов, так как если будем делать это посре­дине ком­на­ты, может полу­чить­ся погреш­ность. Жела­тель­но при­сут­ствие помощ­ни­ка, кото­рый будет при­дер­жи­вать один конец рулет­ки. В про­тив­ном слу­чае мож­но закре­пить её каким-то тяжё­лым пред­ме­том или заце­пить за край плинтуса.
• Если дли­на изме­ря­ю­щей лен­ты недо­ста­точ­на, замер при­дёт­ся про­во­дить поэтап­но, фик­си­руя лен­ту и про­став­ляя мет­ки. Затем сум­ми­ру­ем участ­ки дли­ны по про­став­лен­ным мет­кам и полу­ча­ем общий размер.

Напри­мер, дли­на ком­на­ты 5 м, а шири­на — 4 м. Пере­мно­жим эти две циф­ры, полу­ча­ем пло­щадь ком­на­ты — 20 м2 .

Как измерить площадь помещения с нишей

Услож­ним зада­чу: допу­стим в поме­ще­нии име­ет­ся пря­мо­уголь­ная ниша. В этом слу­чае раз­би­ва­ем ком­на­ту на два пря­мо­уголь­ни­ка боль­шой и малень­кий. Изме­рить нуж­но будет две сто­ро­ны боль­шо­го и две сто­ро­ны малень­ко­го прямоугольника:

• дли­ну мень­шей сто­ро­ны ком­на­ты (рас­сто­я­ние до ниши) а1;
• шири­ну ком­на­ты — b1;
• дли­ну и шири­ну ниши а2 и b2 .

Пло­щадь ком­на­ты будет рав­но сум­ме най­ден­ных пло­ща­дей двух пря­мо­уголь­ни­ков: S = а1* b1   + а2 * b2.

Рас­счи­та­ем пло­щадь ком­на­ты на рисун­ке ниже.

Здесь: а1 = 4.35 м; b1 = 5 м; а2 = 2.65 м; b2 = 2.5 м.

S = 4.35 * 5 + 2.65 * 2.5 =21.75 +6.625 = 28.375 м2.

Как рассчитать площадь комнаты любой формы

Прин­цип рас­че­та оди­на­ков для поме­ще­ний любой формы:

Для вычис­ле­ний доста­точ­но знать сле­ду­ю­щие формулы:

• S пря­мо­уголь­ни­ка = a * b (1), здесь и далее а и b — дли­на и шири­на помещения.
• S пря­мо­уголь­но­го тре­уголь­ни­ка (это поло­ви­на пря­мо­уголь­ни­ка), то есть S тре­уг. = a * b /2 (2);
• S кру­га = π*r2 (или π*d2 / 4) (3) , где π = 3.14, r и d — ради­ус и диа­метр окружности;
• S полу­кру­га = π*r2 /2 (4);
• S тра­пе­ции с осно­ва­ни­я­ми а, b и высо­той h: S трап. = (а + b)/2 * h (5).

Что такое квадратный метр

Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.

Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.

Основные понятия

Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

Свойство аддитивности площади

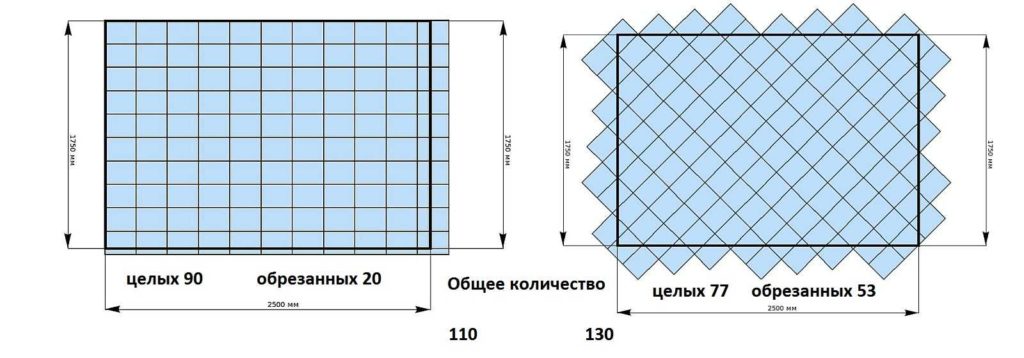
Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

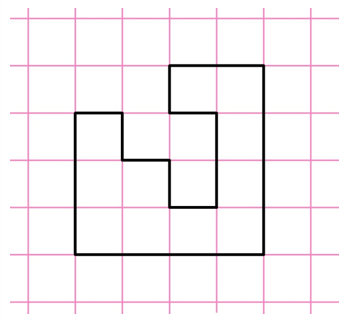
Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

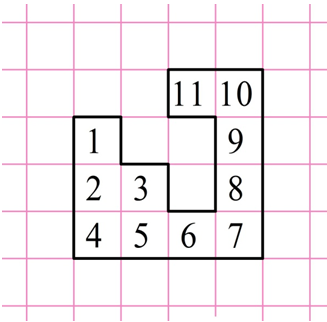
В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

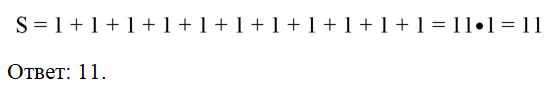
Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

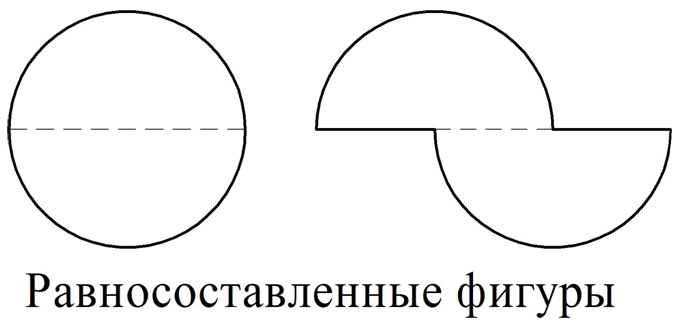
Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут

Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны

Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

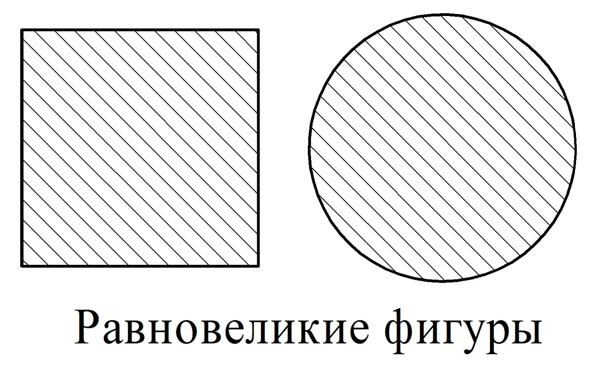
С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

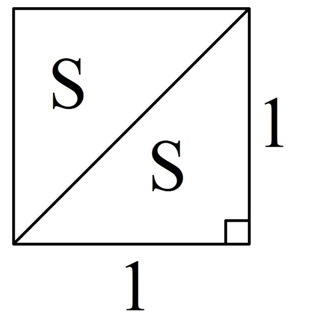
Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

• площадь квадрата со стороной 1 равна единице:
• равносоставленные фигуры имеют равную площадь.

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Соотношение между единицами измерения площадей

Площадь измеряется в «квадратных» величинах: м2, см2, км2 и т.д. Как связаны эти единицы измерения? Для ответа на этот вопрос построим квадрат со стороной 1 см и разобьем каждую его сторону на отрезки длиной 1 мм. Естественно, что таких отрезков будет 10, ведь, в 1 см равен 10 мм. Далее разобьем большой квадрат на маленькие, их число будет равно 102 = 100:

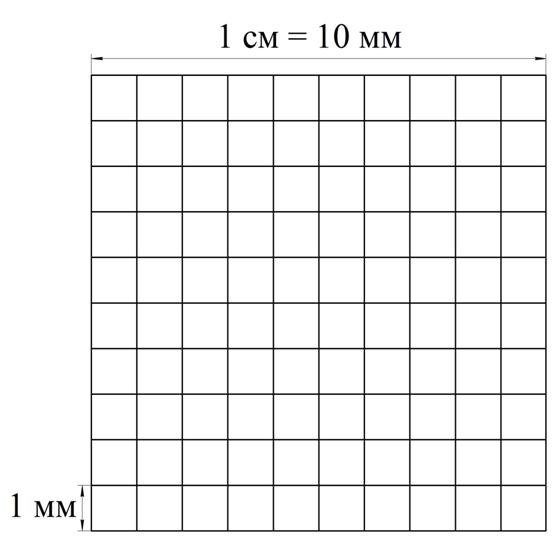
Площадь большого квадрата равна 1 см2, а площадь маленьких составляет 1 мм2. Так как большой квадрат состоит из 100 маленьких, мы можем записать:

Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:

В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:

Задание. Площадь окружности равна 24 см2. Выразите эту величину в мм2 и м2.

Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см2 равен 100 мм2:

Характеристики понятия

Площадь имеет несколько характеристик:

• Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.

• Нормируемость.

  Что это значит? Это значит, что у площади есть какая-то норма, с которой и сравнивают поверхность любой фигуры. Норма площади это квадрат со сторонами 1 на 1. Если это квадрат со сторонами 1 на 1 см, то единица измерения площади будет называться см квадратный и т.д.

• Если две фигуры объединить, так, что они не будут иметь общих внутренних точек, то есть совместить фигуры по какой-либо стороне, то площадь получившейся фигуры будет равна сумме площадей двух изначальных фигур.

На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.

Как высчитать квадратный метр: нюансы, которые следует обязательно знать

Чаще всего при указании квадратуры упаковки того или иного строительного материала производитель приводит квадратные метры. Система СИ принята во многих странах. Как рассчитать квадратный метр? Можно вычертить квадрат с метровой стороной. В этом случае поверхность, очерченная данным квадратом, и будет равна квадратному метру. Большинство измерительных приборов позволяют получить результаты измерения сразу в квадратных метрах.

Квадратный метр найти несложно

Кроме квадратных метров можно использовать и другие единицы измерения. При наличии онлайн-калькулятора расчет квадратных метров значительно упрощается. Однако при желании перевод можно выполнить самостоятельно, умножив имеющееся значение на соответствующий коэффициент, можно найти искомое значение. Для начала следует определить с новой единицей измерения. Если это:

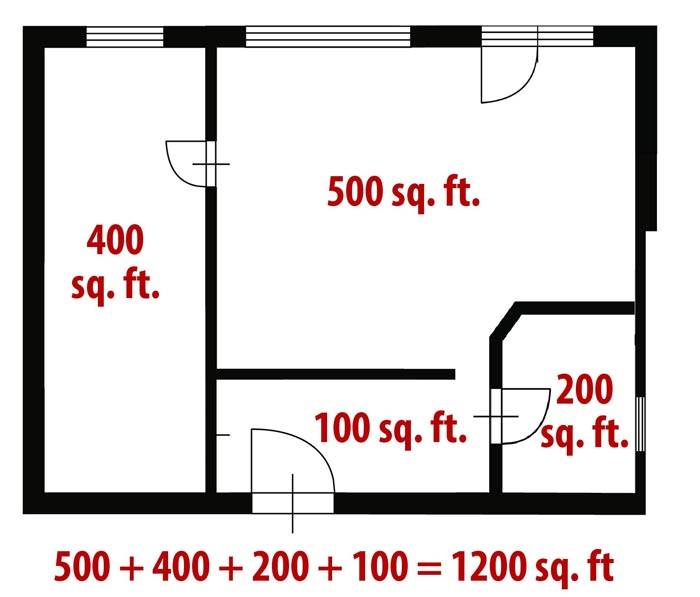
Для перевода из квадратных футов в метры умножаем на 0,093

• Ярды. Коэффициент равен 0,84. Перевод ядров в квадратные метры выполняется по алгоритму, описанному выше. Для более точных расчетов можно использовать поправочный коэффициент 0,83613;
• Акры. При расчете квадратуры помещения такие единицы измерения используются редко, так как один акр равен 4050 квадратным метрам. Однако при необходимости перевод можно сделать с помощью поправочного коэффициента 4050 (4046,9 при более точном расчете).

Акр используется при определении квадратуры земли

Возможно использование и других единиц

При переводе площади важно помнить, что речь идет о квадратах, а потому используется не соотношение линейных размеров, а площадей. Найти поправочный коэффициент в этом случае достаточно просто. Если известно, что метр и искомая единица измерения соотносятся как коэффициент К, то поправочный коэффициент будет численно равен К²

Если известно, что метр и искомая единица измерения соотносятся как коэффициент К, то поправочный коэффициент будет численно равен К².

Калькулятор расчета площади земельного участка неправильной формы

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Калькулятор расчета площади земельного участка неправильной формы Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна

Что нужно, чтобы рассчитать площадь стен?

Рассчитать площадь стен дома можно либо онлайн, либо вручную. Второй вариант более трудоемкий, но точный и подходит в случае, если нет доступа к интернету по тем или иным причинам. Для расчетов потребуется:

• карандаш или ручка;
• листок бумаги;
• калькулятор;
• длинная линейка;
• уровень;
• рулетка.

Важно!
Зная точную площадь стен и помещения, можно приобрести нужное количество строительных материалов, необходимых для ремонта. Площадь измеряют квадратными метрами и обозначают м2.. На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы

И по мере получения замеров, их наносят на чертеж

На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы. И по мере получения замеров, их наносят на чертеж.

Площади простых фигур

Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.

Рассмотрим наиболее популярные формулы определения площадей:

• Прямоугольник. S=a*b – произведение длины на ширину.
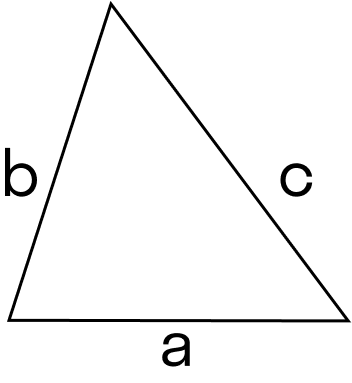
• Треугольник. $S={1\over2}a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
• Круг. $S=\pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.

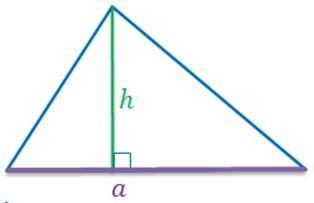
Рис. 1. Высота в произвольном треугольнике.

Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.

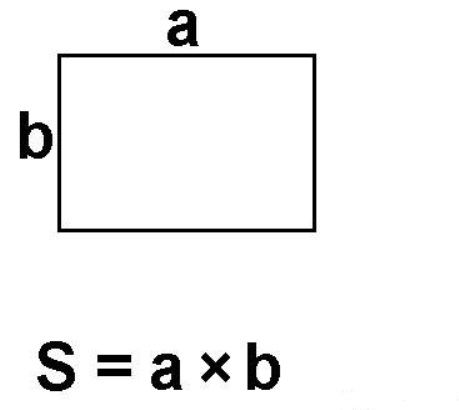
Рис. 2. Площадь прямоугольника.

Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:

$$S=a^2$$

Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:

$$1га=100м∙100м=10 000м^2$$

Площади полей могут также измерять в арах, что в народе называют «соткой», потому что один ар – это квадрат, сторона которого равняется 10 м, а его площадь соответственно 100 $м^2$.

$$1 ар=100м^2$$.

Как высчитать площадь пола с неправильными размерами?

Если комната имеет нестандартные размеры — вычисление площади пола будет происходить немного дольше и сложнее. Существует множество причин, по которым комната может иметь нестандартные формы, например, ниша в спальне или встроенный шкаф. Стоит заметить, что способ найти площадь нестандартного пола все же можно. Для этого необходимо разбить помещение на небольшие геометрические фигуры, например, треугольники, квадраты, прямоугольники и т. д. Конечно, есть множество других способов, как рассчитать площадь пола, но с помощью такого способа — это сделать намного проще.

После того, как помещение будет разделено на геометрические фигуры, можно легко узнать их площадь, перемножив стороны одну на другую. После всех расчетов, площади фигур необходимо сложить, таким образом можно узнать точную площадь.

Среди прочих способов, как можно высчитать площадь пола, достаточно посмотреть жилую и общую площадь в домовой книге, если домовой книги нет — в плане застройщика.

Заключение

Теперь мы знаем, как правильно рассчитать площадь стен и можем, согласно полученным данным, закупить необходимое количество отделочного материала. Даже если ремонт будут осуществлять специальные квалифицированные бригады, то вы всегда сможете проверить правильность их расчетов.

Поскольку клиент оплачивает стоимость ремонта за каждый квадрат, а сторонние подрядчики частенько считают в свою пользу, не учитывая окон и дверей, то эти знания помогут вам существенно сократить стоимость ремонта, особенно при использовании дорогих отделочных материалов. Для полной уверенности рекомендуется проводить все замеры дважды, что позволит избежать возможной ошибки.

Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.

Для расчетов понадобятся:

• уровень строительный;
• рулетка с ограничителем;
• длинная линейка и угольник;
• карандаш и бумага;
• калькулятор.

Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.