Как посчитать неравносторонний прямоугольник

Вычисление площади пола

Если комната стандартная (квадратная или прямоугольная), то вычислить площадь такого помещения сможет каждый. Для этого нужно узнать ширину и длину помещения, после чего просто перемножить эти показатели.

Таким образом, формула будет выглядеть так: S = a * b, где, а и b — длина и ширина помещения.

Если вы рассчитываете площадь помещения для потолка, то встроенные шкафы или камины никак не повлияют на замеры площади.

В случае, если вы собираетесь установить камин или же установить встроенный шкаф-купе, то площадь, которую он будет занимать, нужно обязательно вычислить исходя из предполагаемых размеров конструкции и общих размеров помещения.

Проводить точные замеры помещений, в которых имеется встроенная мебель, необходимо, если вы планируете укладывать напольное покрытие. В случае, если камин или комод занимает не много места, его площадью можно пренебречь, если много — конструкцию на время можно разобрать или высчитать сколько места она занимает.

Площадь участка сложной формы

Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).

Длина стороны A

Длина стороны B

Длина стороны C

Длина стороны D

Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя. Надеюсь, эта демонстрация поможет понять это всем, кто просил создать для этого калькулятор.

Зачем нужно знать площадь полаОпределение площади прямоугольного помещенияРасчет площади комнаты неправильной планировкиУзнаём площадь треугольного помещенияКак рассчитать площадь стен комнатыКак рассчитать площадь стен комнатыПропорции между площадью пола и окон

Невозможно проводить ремонт напольной поверхности, не зная точную площадь пола в частном домовладении или квартире. Дело в том, что сегодня стоимость строительных материалов достаточно высокая, и каждый владелец недвижимости старается максимально сэкономить на их покупке. Поэтому информация, как рассчитать площадь пола, не будет лишней для того, кто предпочитает делать ремонт собственноручно.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

1. Найти квадрат радиуса (умножьте радиус на радиус).
2. Умножить квадрат радиуса на 4.
3. Найти квадрат известной стороны.
4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
5. Найти квадратный корень разности.
6. Умножить корень на известную сторону.

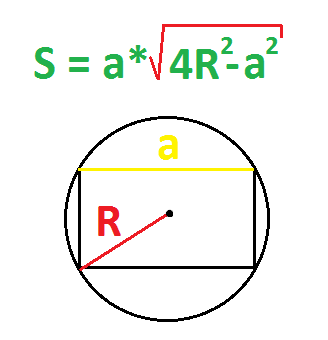
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

1. Квадрат радиуса: 5*5=25 см.
2. Четыре квадрата радиуса: 4*25 = 100 см.
3. Квадрат стороны: 6*6 = 36 см.
4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Как высчитать метр квадратный: единицы изменения

При расчете площадей потолка, пола и стен, необходимо выяснить, как рассчитать квадратный метр. Для вычислений необходимо выбрать мерную ленту или рулетку с нанесением делений в сантиметрах или метрах. Такое приспособление применяются для площади в квадратных метрах.

Если величина получается больше метра, то используются не только метры, но и сантиметры.

Чтобы правильно провести расчеты можно воспользоваться калькулятором квадратных метров. При необходимости померить всю длину, можно делать это поэтапно. Например, сделать отметку там, где закончилась рулетка, а затем протянуть ее еще раз.

В таблице представлены распространенные единицы измерения площади

Ширина меряется также рулеткой. При этом ее располагают под углом в 90 градусов к длине. Если длина меньше метра, то необходимо округлить в сторону ближайшего сантиметра.

При расчете квадратных метров калькулятором, не всегда получается выполнить измерения в метрах. Показатель отображается, как в метрах, так и в сантиметрах. При этом 1 см равняется 0,01 метра. Например, 98 см равно 0,98 м. То есть можно записать 2,98 м. Чтобы получить площадь нужно длину умножить на ширину. Округлять значение можно в большую сторону.

В таблице перевода величин можно узнать необходимые значения

Стоит отметить и другие единицы измерения:

• в 1 квадратном фунте – 0,093 квадратных метра;
• в ярде – 0,84 кв. м.

Умение правильно посчитать площадь необходимо в таких случаях:

требуется точный расчет материалов для ремонта;
наемные мастера часто проводят расчеты оплаты за квадратный метр, что необходимо перепроверять для исключения обмана;
необходимы знания расчетов при выборе площади

Часто оплата коммунальных услуг вычисляется, исходя из размеров комнаты;
чтобы определить нормативы освещенности также нужно знать габариты помещения;
зная площадь, всегда можно посчитать объем, что очень важно при установке отопительных, вентиляционных и климатических устройств.. Значения для погонного метра

Значения для погонного метра

В ролике дается простое объяснение необходимых значений:

Watch this video on YouTube

Как посчитать площадь комнаты: методика расчета по полу

Можно рассчитать площадь пола. Данная процедура состоит из таких этапов. Прежде всего, необходимо освободить стены помещения. Лучше проводить измерения в пустом помещении. Если помещение прямоугольное, то можно перемножить две стороны

В реальности стороны могут немного отличаться, поэтому так важно мерить все стороны. В некоторых случаях комната может быть не правильной конфигурации

В такой ситуации все пространство делится на отдельные прямоугольники. При этом можно нарисовать схему со всеми размерами. Затем считается площадь отдельных участков. Кстати, помещение не обязательно будет состоять только из прямоугольников. Оно может содержать треугольники и даже круги.

В таблице можно посмотреть соответствие площади на полу с показателями для стен при определенной высоте потолка

Если вы не знаете, как посчитать квадратные метры комнаты, то можно воспользоваться специальным калькулятором. При вычислении габаритов не обязательно соблюдать все размеры до сантиметра. Часто применяется округление значений. Иногда  требуется учитывать разные углубления и выступы в стенах.

При расчетах важно учитывать и их предназначение. Если нужно узнать значения для монтажа теплого пола, то можно не учитывать пространство, занятое тяжелой мебелью

Есть варианты, когда в помещении используются разные уровни пола. В подобной ситуации также требуется поделить комнату на отдельные зоны. Не стоит осуществлять замеры по стене, так как она может иметь кривую поверхность.

Сложно определить площадь по полу, имеющего разнообразные выступы в виде волн или полукругов.

Полы сложной конфигурации требуют особой внимательности и использования специальных формул

Расчёт площади помещения.

Этот строительный калькулятор поможет вам точно рассчитать площадь стен и полов, в помещении любой планировки, вычитая двери о окна.

Выберите планировку помещения: (щёлкнув по картинке)

Неплохо это показать на примере конкретных цифр.

Сообщение #3 11/3/2015 21:18

Здравствуйте! Ваш калькулятор действительно некорректно считает. Мои данные: Высота стен -2,56м Стена #1 -1,87м Стена #2 – 2,05м Ширина двери 0,75м Высота двери 2м

Итого исходя из Ваших расчетов:

Площадь полов или потолка – 2 m2 Площадь стен – 15.3 m2 Верхний периметр – 6 п.м. Нижний периметр – 6 п.м. Откосы окна – 0 п.м. Откосы двери 4 п.м.

Сообщение #4 11/3/2015 21:24

Здравствуйте еще раз. Я прошу прощения! Все правильно считает!! Главное десятые и сотые писать через точку, а не через запятую!! Спасибо за калькулятор

Сообщение #5 12/3/2015 8:46

Сделаю так, чтобы запятая заменялась точкой при не правильном вводе. Спасибо за отзыв

Сообщение #6 19/3/2015 0:48

Калькулятор считает правильно. Просто не понимает запятые и не учитывает цифры после них. Если ставить точки то всё правильно получается.

Сообщение #8 16/5/2015 9:09

Версия 2.0 Появилась возможность вводить несколько размеров окон и дверей. Правильно считает если в числе поставленна запятая.

Сообщение #13 6/12/2015 9:53

При нпжатии сохранить никакой реакции программы. Непонятно о чём речь? Если про андроид приложение, то: При сохранении в программе – появится надпись ГОТОВО, результаты хранятся в закладках (стартовый экран программы). Если в телефоне – указан путь хранения текстового файла, который ищите через проводник телефона в папке calculator-m2/

Сообщение #15 6/12/2015 19:35

Специально удалил свою версию и купил свою программу в ГуглПлей. как Вы описали – папка SMETA создаётся, а значит и файлы в ней!

Вот Вы делаете расчёты.

При сохранении Вам покажут расчёты (вверху будет путь к файлу). Эта информация сохраняется в памяти телефона ввиде *txt файла.

Тут ищем нужный файл.

Сообщение #19 1/12/2016 6:19

Было бы не плохо иметь возможность редактировать представленные в программе виды планировки комнат (добавлять или убирать стены и перегородки), так как комнаты могут быть нестандартные и не подходящие ни к одному из представленных видов.

Сообщение #20 15/1/2017 14:31

здраствуйте разработчики рограма прораб очень хорошая на 5 . я поставил вам одну звеоздочку только для того чтобы вы ме ответили.я купил у вас прогу и всео окей пока я не поменял планшет

Сообщение #22 27/9/2017 16:09

зачетный калькулятор! Умел бы еще считать нижний периметр , вычитая из него ширину дверных проемов ^^

Расчёт площади помещения Расчёт площади помещения. Этот строительный калькулятор поможет вам точно рассчитать площадь стен и полов, в помещении любой планировки, вычитая двери о окна. Выберите планировку помещения:

Определение площади плоской фигуры взвешиванием

Определение площади плоской фигуры взвешиванием. Ход работы: Вырезаем из картона фигуру неправильной формы и квадрат со стороной 10 см. Определяем площадь квадрата: Sкв = 100 см2. Определяем массу фигур: масса фигуры неправильной формы: m1 =…г; масса квадрата: mкв =…г. Определяем площадь фигуры неправильной формы: S1= m1/mкв · Sкв= (см2) Вывод: площадь плоской фигуры неправильной формы: … см2.

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Различные способы нахождения площади фигур неправильной формы.ppt» можно в zip-архиве размером 3590 КБ.

краткое содержание других презентаций на тему слайда

«Геометрия 8 класс площади» — В жизни часто математические знания помогают решать производственные задачи. Вычислить площадь прямоугольника. 2. Устная работа. Сдача работы. Повторить и закрепить формулы площади квадрата и прямоугольника. Урок «Делаем ремонт» по теме «Площади» (геометрия 8 класс). Вычислить площадь прямоугольника со сторонами 8 см и 15 см.

«Площадь прямоугольника» — Формула площади прямоугольника. Равные фигуры – равные площади. Если фигуры равновеликие, то они равны. Равные фигуры имеют равные площади. Площадь прямоугольника. Равновеликие фигуры. Найдите длины сторон представленных прямоугольников и их площади. Фигуры, имеющие равную площадь, называются равновеликими.

«Симметрия геометрических фигур» — Квадрат. Круг. Прямоугольник. Когда красота притягивает, а исследование увлекает. Разносторонний треугольник. Равносторонний треугольник. Окружность имеет бесконечно много осей симметрии. Слово «симметрия» в переводе с греческого означает «одинаковость в расположении частей». Неразвернутый угол. Параллелограмм.

«Трафальгарская площадь» — История площади. Отдых на площади. Одна из лучших -первомайская. Трафальгарская площадь. Вся Трафальгарская площадь заполнена людьми, снующими туда-обратно. На Трафальгарская площадь очень много голубей. Трафальгарские демонстрации.

«Понятие площади» — Тематическое планирование зачетов. ИГРА «Умники и Умницы». Тема: «Окружность» №4. (1час). Учащимся предварительно сообщается примерный перечень заданий, выносимых на зачет. Материал по теме усвоен, настроение приподнятое. Реализовать триединые дидактические задачи: через использование различных уровней обучения.

«Площадь треугольника 8 класс» — Sanc : sank = aс: ak, sanc : sank = ас : mk (2). Площадь треугольника. Треугольники АВС и АNC имеют общую высоту СН. Следствия. Доказательство: Основания и высоты треугольника. Соотношение между сторонами и высотами треугольника. Равные многоугольники имеют равные площади. SABC : SANC = AB : AN, SABC : SANC = AB : MN (1).

Узнаём площадь треугольного помещения

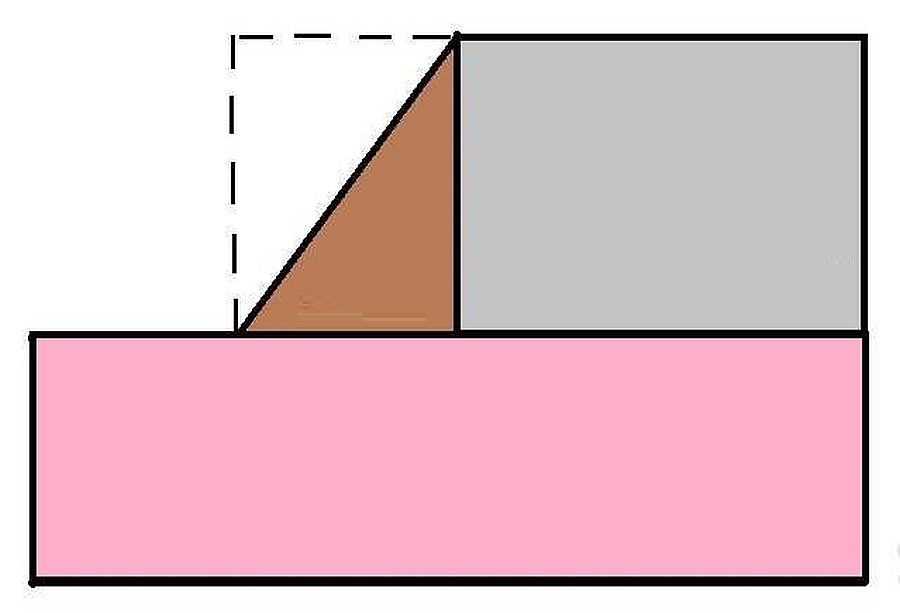
Когда другая часть комнаты располагается не перпендикулярно относительно основной площади, это означает, что между двумя прямоугольниками присутствует еще и треугольник, имеющий прямой угол.

В данном случае площадь треугольника вычисляют по формуле: S = (a х b):2 и прибавляют к общему итогу. Например, а = 2, b = 3, тогда S = (2х3): 2 =3 м².

Можно иначе определить площадь:

1. Прежде вычисляют квадрату прямоугольника.
2. Определяют площадь скошенного треугольного угла.
3. Из квадратуры прямоугольника вычитают площадь треугольника.

В том случае, когда треугольник не имеет прямого угла, тогда используют формулу Герона S = √p(p — a)(p — b)(p — c).

Например, стороны его равны 5, 6 и 7 метров, тогда вычисления производят следующим образом:

1. Узнают полупериметр треугольника p = (5+6+7):2 = 9.
2. В формулу Герона подставляют цифровые значения и получают результат: √(9 х(9-7) х(9-6)х(9-5) =14,7 м².

Что такое прямоугольник

Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.

Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:

Зачем нужно знать площадь пола

Прежде чем приступить к работе, следует определиться с объемом мероприятий, запланировать затраты и рассчитать количество стройматериалов. Для этого нужны будут исходные данные

По этой причине важно знать, как посчитать площадь пола безошибочно. Особенно это касается неровных поверхностей и помещений, имеющих нестандартную планировку

Встречаются и другие причины, когда имеется потребность точно определить размеры поверхности пола:

• проверка качества выполнения строительных работ;
• необходимость проведения перепланировки помещения.

В данной статье рассказывается, как посчитать площадь пола в квадратных метрах в комнатах, имеющих разную конфигурацию.

Использование штриховки

Данный способ максимально прост и является самым популярным среди пользователей программы Автокад, потому что требуется выполнить лишь следующие действия:

1. Заполните штриховкой область. Штриховка должна наноситься на какой-то определённый объект. Если же штриховкой будут заполнены несколько фигур или областей, «S» суммируется. Это к слову, ответ к вопросу о том, как узнать или как найти площадь нескольких фигур сразу. Выбор штриховки, её внешний вид и остальные параметры подбираются лично вами, на точность определения они никак не влияют.
2. Вызовите уже упомянутое ранее «Свойство», нажав «ctrl+1».
3. И всё в том же блоке «Геометрия» и можно ознакомиться с подсчётами площади штриховки, заполняемой фигуры или объектов.

Как найти площадь неправильной фигуры

Инструкция

Получится 2(12/у+у)=14. Перенесите подобные 12/y+y=14/2. 12/у+у=7. Умножьте обе части уравнения на «у». Получится 12+у^2=7у. у^2-7у+12=0 – квадратное уравнение, считайте через дискриминант. У уравнения 2 корня у=4; у=3.

Вычисление сторон равностороннего треугольника. Для того чтобы узнать его сторону (а все его стороны равны), помимо площади необходимо знать высоту. Если известны две эти величины, то расчет можно совершить по этой формуле: b=2S/h, где b – сторона треугольника, S – площадь, h – высота. Пример: Пусть площадь равностороннего треугольника ABC равна 25. Высота BH = 5.Подставьте значения в формулу: b=2*25/5. Ответ: сторона равна 10.

Обратите внимание

Расчет сторон остальных фигур, имеющих стороны различные по длине друг к другу, требует знания большего количества величин.

Как посчитать необходимое количество плитки

Для того, чтобы узнать необходимое количество плитки, необходимой для укладки в той или иной комнате, необходимо узнать площадь помещения. Как быстро найти площадь пола любой комнаты — описано выше. После того, как площадь будет рассчитана, необходимо узнать площадь 1 плитки из выбранной коллекции. После этого нужно просчитать, сколько плиток необходимо для укладки её в комнате.

• Площадь комнаты: 20 м2,
• Размеры плитки: 0,2 х 0,4 м,
• Площадь 1 плитки: 0,08 м2,
• Необходимое количество плиток: 250.

Таким способом можно узнать количество необходимой плитки. Таким же способом можно рассчитать необходимое количество паркетной доски или ламината. Стоит заметить, что в некоторых случаях количество необходимых материалов зависит от узора, который будет выполнен на напольной поверхности.

Для того, чтобы правильно рассчитать площадь пола — необходимо знать геометрические формулы или же уметь пользоваться онлайн калькулятором.

Данные по площади пола можно узнать из домовой книги. Комнаты, которые имеют сложную геометрическую форму проще всего рассчитывать с помощью деления их на небольшие геометрические объекты.

Узнать площадь полукруглой поверхности можно с помощью формулы: S = πR2/2 — радиус круга.

Для того, чтобы напольный материал не пришлось покупать еще — добавьте до необходимого количества 10%. Если вы правильно вычислите необходимое количество материалов — вы сможете качественно и надежно уложить любое напольное покрытие.

Как считать площадь пола: подробное руководство и калькулятор Подробное руководство и примеры, как посчитать площадь пола в квартире. Практическое предназначение расчетов. Их наиболее простое выполнение.

Определение площади

Существует несколько способов такого определения площади участков земли:

Наиболее точным из этих методов является аналитический. Это связано с тем, что при его использовании на точность результатов влияют только ошибки полевых измерений, тогда как на два других метода оказывают влияние ошибки плана или карты, с которых снимаются данные.

Расчет площади аналитическим методом

При использовании аналитического способа площадь определяется по данным полевых измерений или по координатам поворотных точек, являющихся функциями результатов полевых измерений.

Участки имеют разные геометрические формы. В частности, они могут иметь четырехугольную форму.

Такая форма участка часто существует в старых садоводческих товариществах, в которых нарезались участки в 6 соток.

Если участок имеет форму трапеции и известны основные параметры такой фигуры, то площадь участка может быть рассчитана по формуле:

• a и b — основания фигуры,
• h – высота трапеции.

Если известны координаты поворотных точек , то площадь надела может быть определена по приведенной ниже общей формуле для многоугольника. При этом для трапеции расчет площади производится по формуле с учетом того, что n=4.

При расчете четырехугольника неправильной формы, когда известны величины каждой из его сторон, необходимо определить величину периметра 2p:

a,b,c,d — величины сторон.

Тогда площадь участка Sнф будет равна:

В формуле используется значение половины периметра p.

Если участок имеет форму многоугольника с n сторонами, то его площадь рассчитывается по координатам поворотных точек:

• Xi и Yi — координаты i-той поворотной точки участка, имеющего вид многоугольника,
• i — порядковый номер точки. Этот параметр меняется от 1 до n,
• n — число характерных точек.

Для проверки правильности расчетов используется другая формула:

Если расчеты проведены правильно, то Sу1 = Sу.

В этом случае аналитический расчет площади участка производится с использованием данных об углах азимута. При этом по контуру границ участка производится замер азимута каждой поворотной точки. Также определяется расстояние от одной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади земельного надела.

Налог при сдаче квартиры в аренду — это тема нашего подробного материала!

Как быстро получить комнату в общежитии и кто из жильцов имеет на это полное право? Узнайте всю необходимую вам информацию в нашей статье.

Хотите безопасно оплатить покупку квартиру и не пострадать от мошенников? Наша статья вам поможет!

Полезные команды и переменные

Полезные команды и переменные:

• «БЫСТРКАЛЬК» – вызов калькулятора;
• «ДИСТ» – для определения расстояния между точками;
• «DISTANCE» – для хранения значений, полученных с применением не особо сложной команды «ДИСТ»;
• «ИЗМЕРИТЬГЕОМ» – для измерения расстояния выделенных объектов или точек;
• «ОКНОСВ» – для вызова свойств объектов;
• «AUPREC» – управление точностью отображения координат;
• «МАСС-ХАР» – для проведения расчётов массовых характеристик 2D областей или 3D тел.

Тем, у кого всё же остались теоретические сомнения о том, как вычислить площадь в Автокаде, следует проверить их на практическом применении, где можно будет убедиться, что все эти действия элементарны.

Комната неправильной формы

Когда нужно рассчитать площадь комнаты неправильной формы, ее разделяют на простые фигуры — квадраты, прямоугольники, треугольники. Далее вымеряют размеры, совершают расчеты по известным формулам. Сначала также проводим обмеры комнаты. Только в этой ситуации цифр будет не 2, а 4: появится еще длина и ширина выступа.

Расскажем на этом примере как рассчитать площадь комнаты неправильной формы с выступом:

• Находим сначала площадь помещения без выступа: 8,5 метров умножаем на 3,6 метров = 30,6 м².
• Считаем площадь выступающей части: 3,25 метров умножаем на 0,8 метров = 2,6 м².
• Складываем обе полученные цифры: 30,6 м² плюс 2,6 м² = 33,2 м².

Существуют комнаты со скошенными стенами. В такой ситуации вам нужно разбить помещение так, чтобы получились прямоугольники и треугольник (показано на схеме ниже).

В этой ситуации считать площадь комнаты нужно так:

• сначала большую прямоугольную часть: 6,4 метра * 1,4 метра = 8,96 м². Округляя, получаем  9 м².
• считаем малый прямоугольник: 2,7 метра * 1,9 метра = 5,13 м². Округляя, получаем 5,1 м².
• далее просчитать площадь треугольника: 1,3 метра * 1,9 метра/2 = 1,235 м². Округляя, получается 1,2 м².
• после найденных величин все складываем, чтобы увидеть общую площадь помещения: 9,0+5,1+1,2=15,3 м².

Современная планировка квартир и домов может быть различной, но общий принцип очень прост. Вы делите помещение на простые фигуры, замеряете все размеры, вычисляете квадратуру каждой фигуры, и все складываем.

Вычислить, найти площадь геометрических фигур

</center>

Онлайн Расчеты и формулы площади для плоских фигур
Площадь треугольника калькулятор нахождения площади треугольников	Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника
Площадь равнобедренного треугольника найти площади равнобедренных треугольников	Площадь равностороннего треугольника вычислить площадь равностороннего треугольника
Площадь треугольника по формуле Герона площадь Герона, формула	Площадь квадрата чему равна площадь квадрата
Площадь прямоугольника как найти чему равна площадь прямоугольника	Площадь круга онлайн калькулятор площади круга через радиуса
Площадь ромба как найти площадь ромба через диагонали и т.д.	Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма
Площадь трапеции площадь прямоугольной и равнобедренной трапеции	Площадь эллипса формула площади эллипса онлайн
Площадь кольца как вычислить площадь кольца онлайн	Площадь четырехугольника чему равна площадь четырехугольника, формула
Площадь сектора кольца подсчитать площади сектора кольца	Площадь сектора круга получить площадь сектора круга
Площадь сегмента круга решить площадь сегмента круга
Онлайн Расчеты и формулы площади для объемных фигур
Площадь шара калькулятор нахождения площадь поверхности сферы или шара	Площадь куба как найти чему равна площадь поверхности куба
Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра	Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды
Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др.	Площадь конуса нахождение площади поверхностей конуса
Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса	Площадь тетраэдра площадь поверхности и грани тетраэдра
Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

Сообщить об ошибке

Математика	Объем фигур	Периметр фигур	Радиус фигур	Единицы измерения площади
Конвертеры	Расход топлива	Теоремы	Угол	Сколько калорий в день

Формула площади прямоугольника

Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.

Рис. 1. Прямоугольник, разбитый на единичные квадраты

Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см2

Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, потому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина

Таким образом, можно вывести формулу площади прямоугольника:

S = a · b, где a,b – ширина и длина фигуры.

К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см2.

Площадь фигур на клетчатой бумаге. Начальный уровень.

Алгоритм нахождения площади фигур на клетчатой бумаге:

Способ 1: (удобен для стандартных фигур: треугольника, трапеции и т.д.)

1. Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади.
2. Подставить найденные значения в уравнение площади.

Способ 2: (очень удобен для сложных фигур, но и для простых неплох)

1. Достроить искомую фигуру до прямоугольника.
2. Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника.
3. Из площадипрямоугольника вычесть сумму площадей всех лишних фигур.

Вывод формул для площадей четырехугольников

      Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d₁ и d₂ – , а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

      Доказательство. В соответствии с рисунком 1 справедливо равенство:

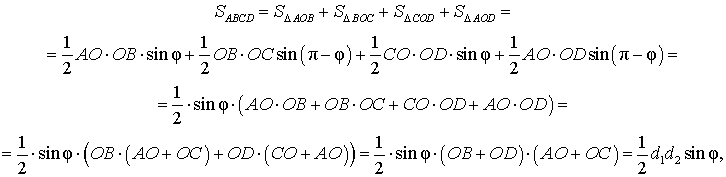
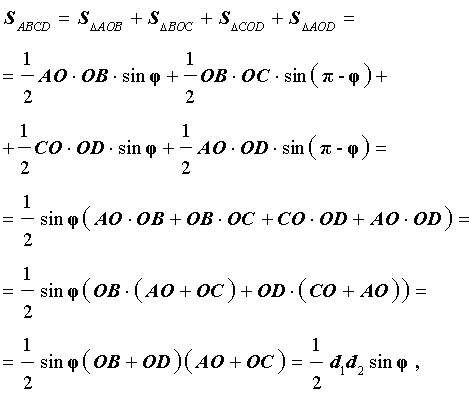
что и требовалось доказать.

      Утверждение 2. Площадь можно найти по формуле

S = a h_a ,

где a – сторона параллелограмма, а h_a – , опущенная на эту сторону (рис. 2).

Рис. 2

      Доказательство. Поскольку (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

S_ABCD = S_AEFD = a h_a ,

что и требовалось доказать.

      Утверждение 3.Площадь можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

      Доказательство. Поскольку

h_a = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a h_a = ab sin φ,

что и требовалось доказать.

      Утверждение 4. Площадь можно найти по формуле

,

где r – радиус , а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

      Доказательство. Поскольку каждая из ромба является биссектрисой угла, а . Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

      Утверждение 5. Площадь можно найти по формуле

,

где a и b – основания трапеции, а h  –  (рис.5).

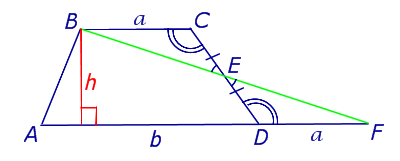
Рис. 5

      Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку , то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь можно найти по формуле

,

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

      Доказательство. Воспользовавшись , составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

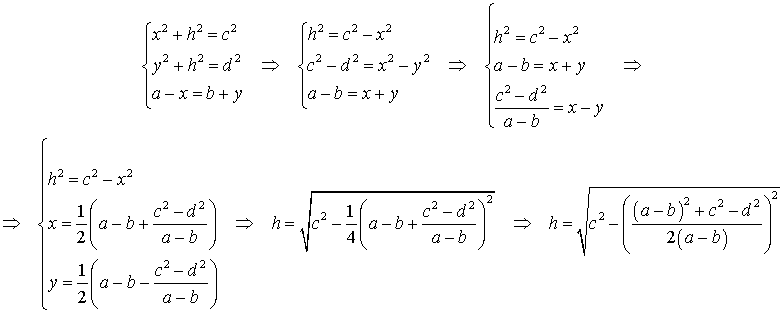
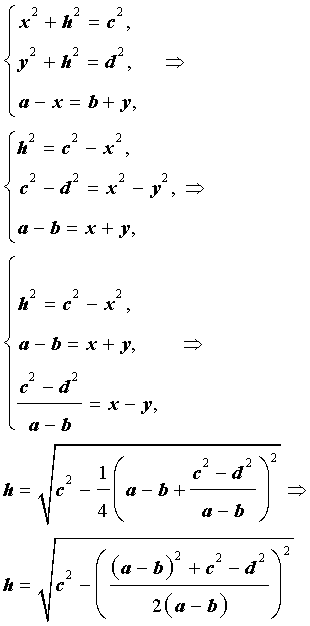
      Следовательно,

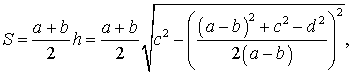
где

,

что и требовалось доказать.

      Утверждение 7. Площадь , , можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус (рис.7).

Рис. 7

      Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

      Если r – радиус вписанной в дельтоид окружности, то

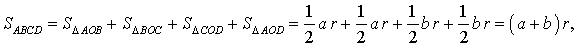
что и требовалось доказать.

Вывод формул для площадей четырехугольников

Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

Доказательство. В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле

S = a ha ,

где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).

Рис. 2

Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

SABCD = SAEFD = a ha ,

что и требовалось доказать.

Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

Доказательство. Поскольку

ha = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a ha = ab sin φ,

что и требовалось доказать.

Утверждение 4. Площадь ромбаромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

Утверждение 5. Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h  – высотавысотавысота (рис.5).

Рис. 5

Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

Утверждение 6. Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

Следовательно,

где

что и требовалось доказать.

Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Рис. 7

Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

что и требовалось доказать.

На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

У нас также для школьников организованы

Заключение

Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

1. S = 1/2*d1*d2*sin(d1,d2);
2. S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
3. S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра​.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.