Калькуляторы расчета размеров развертки конуса

Развертка (выкройка) конуса

• Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
• Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
• Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
• Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
• Следующий калькулятор интересен тем, что он переводит древние российские денежные…
• Следующий калькулятор будет очень полезен тем, кто решил купить или…
• Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
• Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
• Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
• Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
• Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
• Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
• Следующий необычный калькулятор переводит меры длины из русской системы в…
• Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
• Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
• Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
• Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
• Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
• Как вы уже могли заметить на нашем сайте есть несколько…
• Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
• Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
• Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
• Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
• Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
• Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
• Перед вами отличный помощник для IT специалистов. С помощью данного…
• Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
• Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
• Начнем с истории. В 17 веке итальянским ученым Торричелли было…
• Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…

Развертка усеченного конуса

Как мы видели, рассматриваемая фигура образована тремя поверхностями. Две из них представляют основания, а третья является боковой. Сумма площадей этих поверхностей является полной поверхностью усеченного конуса. В трехмерном пространстве ее площадь вычислять неудобно, поскольку сама величина является двумерной. В связи с этим при возникновении проблемы определения площади поверхности пространственных фигур, их принято представлять на плоскости.

В нашем случае развертку получить достаточно просто. Для этого следует мысленно отрезать по соответствующим окружностям основания от фигуры. Затем, необходимо разрезать вдоль образующей и раскрыть поверхность боковую. В итоге получится результат, показанный на фото.

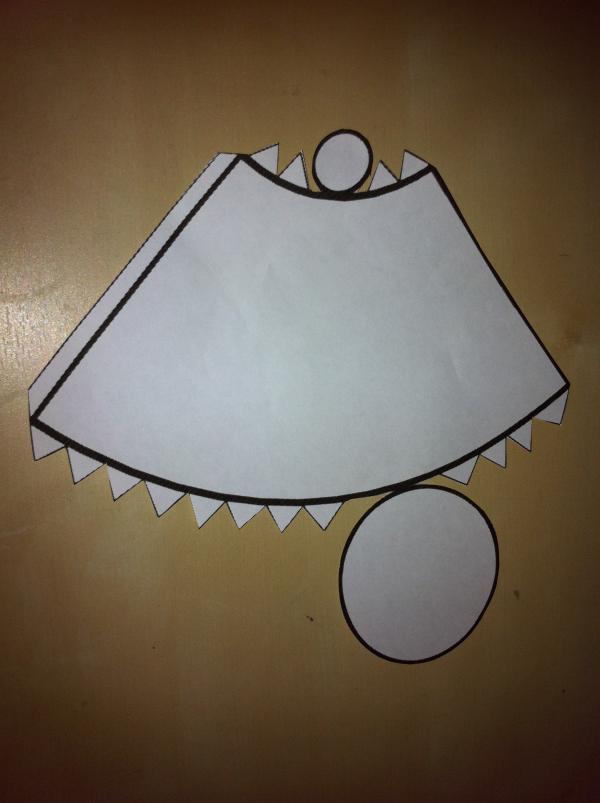
Она представляет собой два разных круга и часть кругового сектора, у которого вырезан центр.

От ровного листа до круглой обечайки:

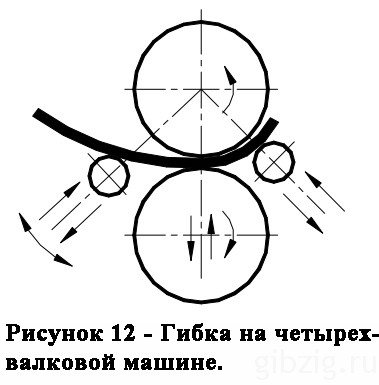
Вальцы с асимметричным расположением валков (рис.11) производят практически полную гибку обечайки. Наиболее современными являются четырехвалковые машины (рис.12), на которых за один цикл осуществляется вальцовка и подгибка краев. Радиус гибки обечаек проверяют шаблонами. Возможные дефекты вальцовки цилиндрических обечаек приведены на рис.14.

Также способы получения нужной формы бывают разные.

Гибка конических обечаек производится несколькими способами:

1) Установкой под углом среднего валка у симметричных трехвалковых машин и бокового валка у асимметричных трехвалковых и четырехвалковых вальцев (рис.15). 2) Гибкой по средней линии последовательно по различным участкам (рис.16) на вальцах. Сначала осуществляют подгибку кромок, затем гнут середину заготовки на каждом участке с переустановками. Такой способ приводит к повышенному износу оборудования. 3) Гибка обечаек на вальцах со сменными коническими валками. Этот способ оправдан в серийном и массовом производстве. 4) Безвальцевым способом для листа толщиной до 20 мм. На рис. 17 показан метод свертывания. Кромки 3 и 4 заготовки закрепляют в опорах 2 и 5, сводят друг к другу, одновременно поворачивают опоры в разных направлениях. Далее кромки конической обечайки соединяют на прихватках и снимают со станка. 5) Наиболее производительным способом является изготовление конических обечаек в штампах (рис.18). Перед сваркой частей обечаек производят их предварительную фиксацию для исключения деформации элементов и обеспечения сварочных зазоров. Совмещение кромок обычно производится струбцинами и сборочными кольцами для тонкого листа (рис.19). На одну обечайку устанавливается две струбцины по торцам. Цилиндричность обечаек обеспечивается специальными приспособлениями с домкратами, распирающими деталь. При сборке габаритных деталей используются стяжные планки и клиновые соединения (рис.20).

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

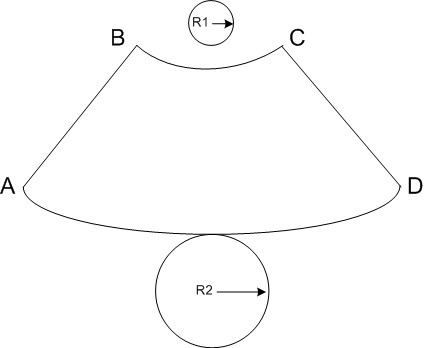
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

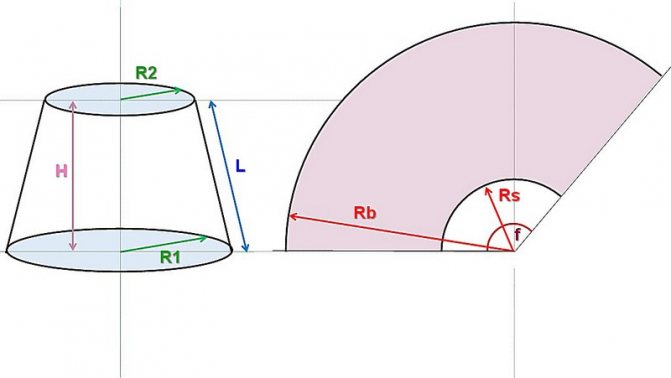
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Бумажный или пластиковый стаканчик

Самый распространенный конический предмет, с которым сталкиваются абсолютно все люди — это стаканчик. Он может быть бумажным или пластиковым, с принтом или без, но неизменным остается одно — это форма! Коническая фома стаканчика была выбрана не просто так, она имеет неоспоримое преимущество перед цилиндрической.

Однако, при необходимости напечатать картинку на конусообразном предмете, возникают некоторые технические и дизайнерские сложности

Сразу обращаю ваше внимание, что стаканчик является усеченным конусом, и далее рассматриваемый способ подготовки принта для печати, будет основан именно на построении макета усеченного конуса и подходит для любых подобных предметов, например, для кружек латте

Усеченный конус и его осевое сечение

Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.

Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r₁ и r₂. Расстояние между основаниями называется высотой, обозначим ее буквой h.

Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r₁ и 2*r₂ соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.

Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r₁, r₂ и h. Соответствующее выражение приобретает вид:

Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r₁ — r₂).

Видео гибки конусной обечайки

После сборки проверяется сварочный зазор и выполняются сварочные прихватки (рис.21). Параметры прихваток приведены в таблице 2. Заходные и выводные планки применяются для обеспечения качественного сварного шва по торцам обечайки.

При сборке обечаек используются роликовые стенды (рис.22) и кантователи. Сварку кольцевых и продольных швов обечаек производят ручным способом, механизированным способом или с применением сварочных роботов. Для ликвидации остаточных напряжений в сварных швах обечайки подвергают термообработке в шахтных печах. После сварки производится калибровка обечайки на вальцах — прокатка ее в несколько заходов. При окончательном контроле изготовленных обечаек проверяют их геометрические размеры, отсутствие деформаций и поверхностных дефектов детали.

Установлен сертификат профессионализма, соответствующий занятию промышленного кипятильника, профессиональной семьи тяжелой промышленности и металлических конструкций, который будет иметь официальный характер и действительность на всей территории страны.

Сертификат профессионализма. Аккредитация учебного контракта. Только переходное положение. Адаптация к национальному учебному и профессиональному плану внедрения. Министр труда и социальных дел настоящим уполномочен издавать такие положения, которые могут потребоваться для осуществления этого Королевского указ.

Более подробно об изготовлении отдельных видов обечаек, читайте в разделах «Вентиляция», «Водосток» и «Для гибки металла».

Вальцовка обечаек – важнейший технологический процесс, без которого нельзя даже представить производство цилиндрических деталей. Рассмотрим более подробно его особенности, технологию и используемый инструмент.

Этот Королевский указ вступает в силу на следующий день после его опубликования в Официальном государственном бюллетене. В Мадриде 24 января. Министр труда и социальных дел. Профессиональный профиль профессии. Для строительства различных элементов используются режущие и формовочные машины, а также электросварочное оборудование, а также организует рабочее оборудование для получения продуктов в условиях безопасности и требуемых качественных характеристик. Построить металлические конструкции.

Построить наборы цилиндрических каналов. Компетентность 1: сборка металлоконструкций. Компетентность 2: построение наборов цилиндрических трубопроводов. Компетентность 3: построение конусов и бункеров. Наблюдение при формовании в горячем состоянии не превышает предельную температуру молекулярной структуры материала.

Осевое сечение конуса и его площадь

Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.

Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:

Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

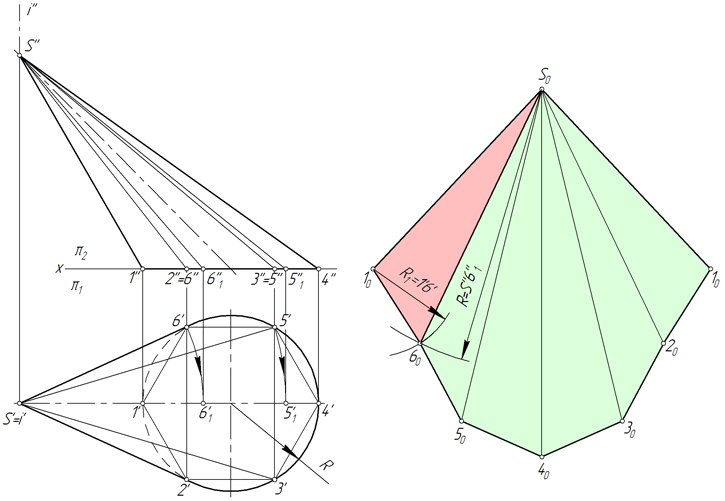
1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

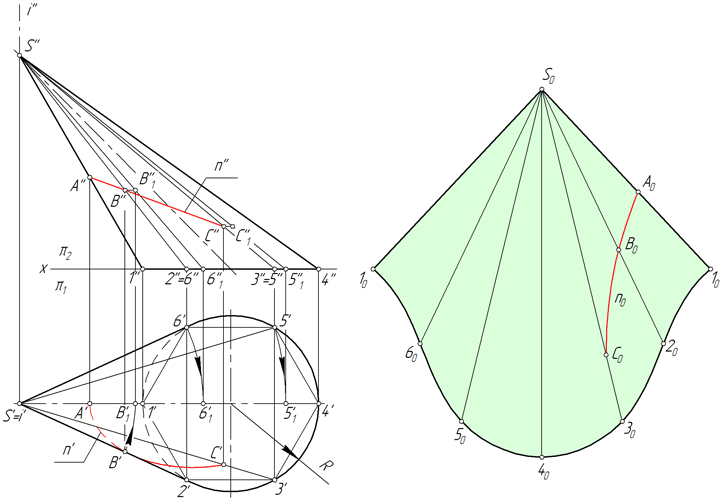
1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
4. Соединяем точки A, B, C плавной линией.

Способы обработки конических поверхностей

При обработке валов часто встречаются переходы между поверхностями, имеющие коническую форму. Если длина конуса не превышает 50 мм, то его обработку можно производить врезанием широким резцом. Угол наклона режущей кромки резца в плане должен соответствовать углу наклона конуса на обработанной детали. Резцу сообщают поперечное движение подачи.

Для уменьшения искажения образующей конической поверхности и уменьшения отклонения угла наклона конуса необходимо устанавливать режущую кромку резца по оси вращения обрабатываемой детали.

Следует учитывать, что при обработке конуса резцом с режущей кромкой длиной более 15 мм могут возникнуть вибрации, уровень которых тем выше, чем больше длина обрабатываемой детали, меньше ее диаметр, меньше угол наклона конуса, чем ближе расположен конус к середине детали, чем больше вылет резца и меньше прочность его закрепления. В результате вибраций на обрабатываемой поверхности появляются следы и ухудшается ее качество. При обработке широким резцом жестких деталей вибрации могут отсутствовать, но при этом возможно смещение резца под действием радиальной составляющей силы резания, что приводит к нарушению настройки резца на требуемый угол наклона. (Смещение резца зависит от режима обработки и направления движения подачи.)

Конические поверхности с большими уклонами можно обрабатывать при повороте верхних салазок суппорта с резцедержателем (рис. 4.32) на угол α, равный углу наклона обрабатываемого конуса. Подача резца производится вручную (рукояткой перемещения верхних салазок), что является недостатком этого метода, поскольку неравномерность ручной подачи приводит к увеличению шероховатости обработанной поверхности. Указанным способом обрабатывают конические поверхности, длина которых соизмерима с длиной хода верхних салазок.

Коническую поверхность большой длины с углом α= 8. 10° можно обрабатывать при смещении задней бабки (рис. 4.33)

При малых углах sinα ≈ tgα

где L — расстояние между центрами; D — больший диаметр; d — меньший диаметр; l — расстояние между плоскостями.

Если L = l, то h = (D-d)/2.

Смещение задней бабки определяют по шкале, нанесенной на торце опорной плиты со стороны маховика, и риске на торце корпуса задней бабки. Цена деления на шкале обычно 1 мм. При отсутствии шкалы на опорной плите смещение задней бабки отсчитывают по линейке, приставленной к опорной плите.

Для обеспечения одинаковой конусности партии деталей, обрабатываемых этим способом, необходимо, чтобы размеры заготовок и их центровых отверстий имели незначительные отклонения. Поскольку смещение центров станка вызывает износ центровых отверстий заготовок, рекомендуется обработать конические поверхности предварительно, затем исправить центровые отверстия и после этого произвести окончательную чистовую обработку. Для уменьшения разбивки центровых отверстий и износа центров целесообразно последние выполнять со скругленными вершинами.

Читать также: Почему мигает энергосберегающая лампа при выключенном выключателе

Достаточно распространенной является обработка конических поверхностей с применением копирных устройств. К станине станка крепится плита 7 (рис. 4.34, а) с копирной линейкой 6, по которой перемещается ползун 4, соединенный с суппортом 1 станка тягой 2 с помощью зажима 5. Для свободного перемещения суппорта в поперечном направлении необходимо отсоединить винт поперечного движения подачи. При продольном перемещении суппорта 1 резец получает два движения: продольное от суппорта и поперечное от копирной линейки 6. Поперечное перемещение зависит от угла поворота копирной линейки 6 относительно оси 5 поворота. Угол поворота линейки определяют по делениям на плите 7, фиксируя линейку болтами 8. Движение подачи резца на глубину резания производят рукояткой перемещения верхних салазок суппорта. Наружные конические поверхности обрабатывают проходными резцами.

Усеченный конус и способы его получения

Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.

Образованная над плоскостью фигура является конусом, а вот фигура под плоскостью — это конус усеченный.

Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.

Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r’.

Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.

Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.

Фигура конус

Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Полученная пространственная фигура имеет следующие характеристики:

1. Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.
2. Сторона AC треугольника — это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.
3. Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.
4. Вершина B треугольника — это вершина конуса.

Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.

От ровного листа до круглой обечайки:

Вальцы с асимметричным расположением валков (рис.11) производят практически полную гибку обечайки.

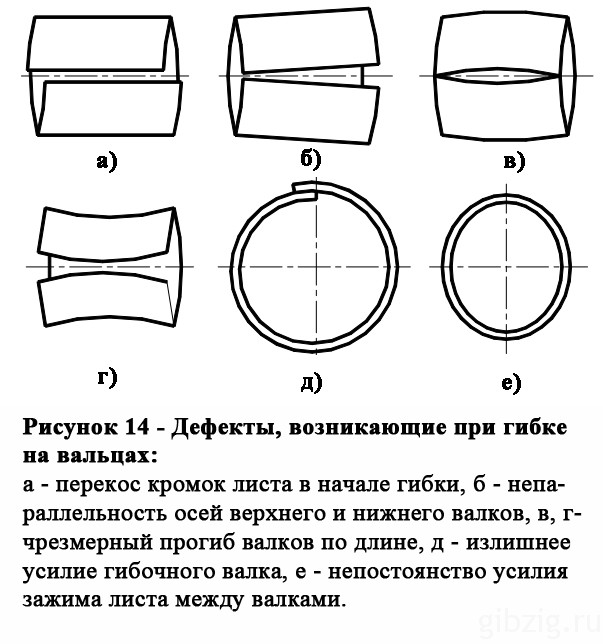
Наиболее современными являются четырехвалковые машины (рис.12), на которых за один цикл осуществляется вальцовка и подгибка краев. Радиус гибки обечаек проверяют шаблонами. Возможные дефекты вальцовки цилиндрических обечаек приведены на рис.14.

Конусы и переходные элементы в каждой прочности и качестве материала

В дополнении к шишкам и переходным частям, мы также производим раковины и доборные любого рода. Компоненты, которые не могут транспортироваться в одной части из-за их размер, мы производим, насколько это технически возможно в ряде сегментов, которые могут быть собраны на месте для получения готового продукта.

Высокая точность и надежность в технологии формирования — как раз вовремя

В производстве мы уделяем большое внимание выдающемуся качеству и точности. Существует много причин, по которым вам может понадобиться сделать конус с металлической фольгой

Металлические конусы служат для запирания дымовых труб, вплоть до определенных видов огня на открытом воздухе и во время барбекю, а иногда и в декоративных целях. Складывание листа металла проще, чем вы могли ожидать, поэтому не пугайтесь процесса

Введите его полностью, но с осторожностью, конечно

Также способы получения нужной формы бывают разные.

Гибка конических обечаек производится несколькими способами:

1) Установкой под углом среднего валка у симметричных трехвалковых машин и бокового валка у асимметричных трехвалковых и четырехвалковых вальцев (рис.15). 2) Гибкой по средней линии последовательно по различным участкам (рис.16) на вальцах. Сначала осуществляют подгибку кромок, затем гнут середину заготовки на каждом участке с переустановками. Такой способ приводит к повышенному износу оборудования.

3) Гибка обечаек на вальцах со сменными коническими валками. Этот способ оправдан в серийном и массовом производстве. 4) Безвальцевым способом для листа толщиной до 20 мм. На рис. 17 показан метод свертывания. Кромки 3 и 4 заготовки закрепляют в опорах 2 и 5, сводят друг к другу, одновременно поворачивают опоры в разных направлениях. Далее кромки конической обечайки соединяют на прихватках и снимают со станка. 5) Наиболее производительным способом является изготовление конических обечаек в штампах (рис.18). Перед сваркой частей обечаек производят их предварительную фиксацию для исключения деформации элементов и обеспечения сварочных зазоров. Совмещение кромок обычно производится струбцинами и сборочными кольцами для тонкого листа (рис.19). На одну обечайку устанавливается две струбцины по торцам.

Цилиндричность обечаек обеспечивается специальными приспособлениями с домкратами, распирающими деталь. При сборке габаритных деталей используются стяжные планки и клиновые соединения (рис.20).

Изготовление рабочего конуса на заказ

Карандаш будет рисовать круг, и небольшая выемка, которая оставила компас там, где она была поддержана, должна быть отмечена. 2 Отрежьте круг специальными ножницами из металлической фольги. Носите перчатки так, чтобы края металла были очень острыми. 3 Отрежьте круг пополам. Используя точку поддержки вашего компаса в качестве ориентира и в качестве конечной точки, разрежьте там прямую линию, начинающуюся с обоих концов. Теперь у вас будет круг металлической фольги с щелью, которая начнется с одной стороны и достигнет центра. 4 Перекройте одну сторону разреза над другой. Начиная с щели, надавите куски листа один поверх другого. При этом вы увидите, что круг начинает сжиматься и формировать конус. Остановитесь, когда это необходимо, в зависимости от того, насколько глубоко вы этого хотите. 5 Лента на каждой стороне оверлея. Это предотвратит перемещение металла и избавит вас от грубых краев. Теперь ваш конус металлического лезвия завершен. Носите перчатки всякий раз, когда вы манипулируете металлическим лезвием, чтобы не обрезать руки. Металлическое лезвие Ножницы для металлического лезвия Компас с карандашом Клейкая лента Перчатки. Установление определенных единообразных правил находит свое разумное значение в необходимости гарантировать в отношении всех профессий, подверженных сертификации, цели, требующиеся сертификатов профессионализма.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

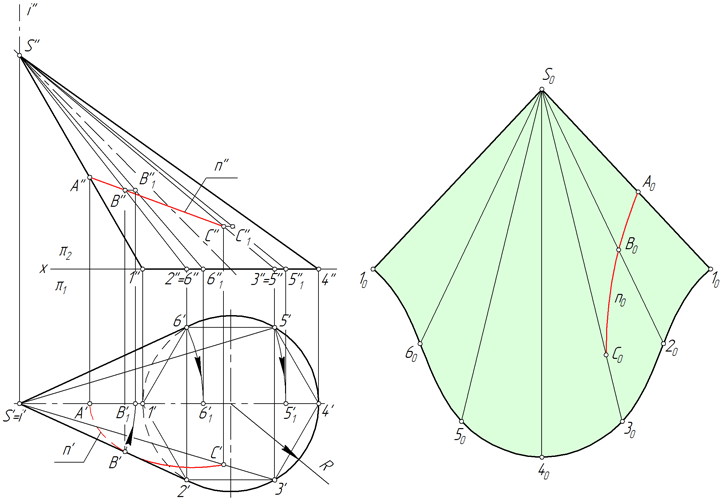
1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
4. Соединяем точки A, B, C плавной линией.

Что ещё можно сделать из бумажного конуса?

Бумажную заготовку для конуса можно использовать, чтобы сделать упаковку для сладкого подарка. Для этого на края, с внутренней стороны, добавляют кусочки двустороннего скотча, или же просто промазывают клеем.

Затем на эти участки помещаются листы гофрированной бумаги.

• Чтобы она красиво легла, нужно делать небольшие складки.
• После этого заготовка с бумагой склеивается в конус.
• Внутрь поделки помещаются конфеты или другие предметы, а гофрированный лист сверху завязывается ленточкой, образуя мешочек.
• На готовую упаковку можно добавить и другие декоративные элементы.

Бумажный конус можно использовать и для других поделок. Например, если делать его из плотного картона, то затем, с помощью ткани, получится создать вот такие игрушки животных или елочное украшение.